Crypto: eXclusive

Challenge Description

One bitwise op is all it takes, fallin’ in love with me

- Halvin Carris and Lua Dipa

Attachments

chal.py

with open('flag.txt', 'r') as f:
    flag = f.read().strip()

with open('key.txt', 'r') as f:
    key = f.read().strip()

extended_key = (key * (len(flag) // len(key) + 1))[:len(flag)]

ct = bytes([ord(f)^ord(k) for f, k in zip(flag, extended_key)])

with open("output.txt", "w") as f:
    f.write(ct.hex())

output.txt

0a06016223376253077e217e3d7b21580776621639796618392d30173e2b62406932

Approach

From chal.py we can observe that the key is read from a file, repeated to match the flag’s length, and then applied byte-wise to the plaintext:

Keep in mind that XOR is symmetric:

We also know from other challenges the flag format starts with RISC{. That gives us a crib (known plaintext) for the first five bytes. We can abuse the crib and the symmetric property of XOR to recover at least 5 bytes of the flag:

Doing that yields:

C[0..4]   = 0a 06 01 62 23
"RISC{"   = 52 49 53 43 7b
xor'd     = 58 4f 52 21 58  →  "XOR!X"

Looks like we have a 4 byte key that repeats - let’s try XOR!:

ct = bytes.fromhex("0a06016223376253077e217e3d7b21580776621639796618392d30173e2b62406932")
key = b"XOR!"
pt  = bytes(c ^ key[i % len(key)] for i, c in enumerate(ct))
print(pt.decode())

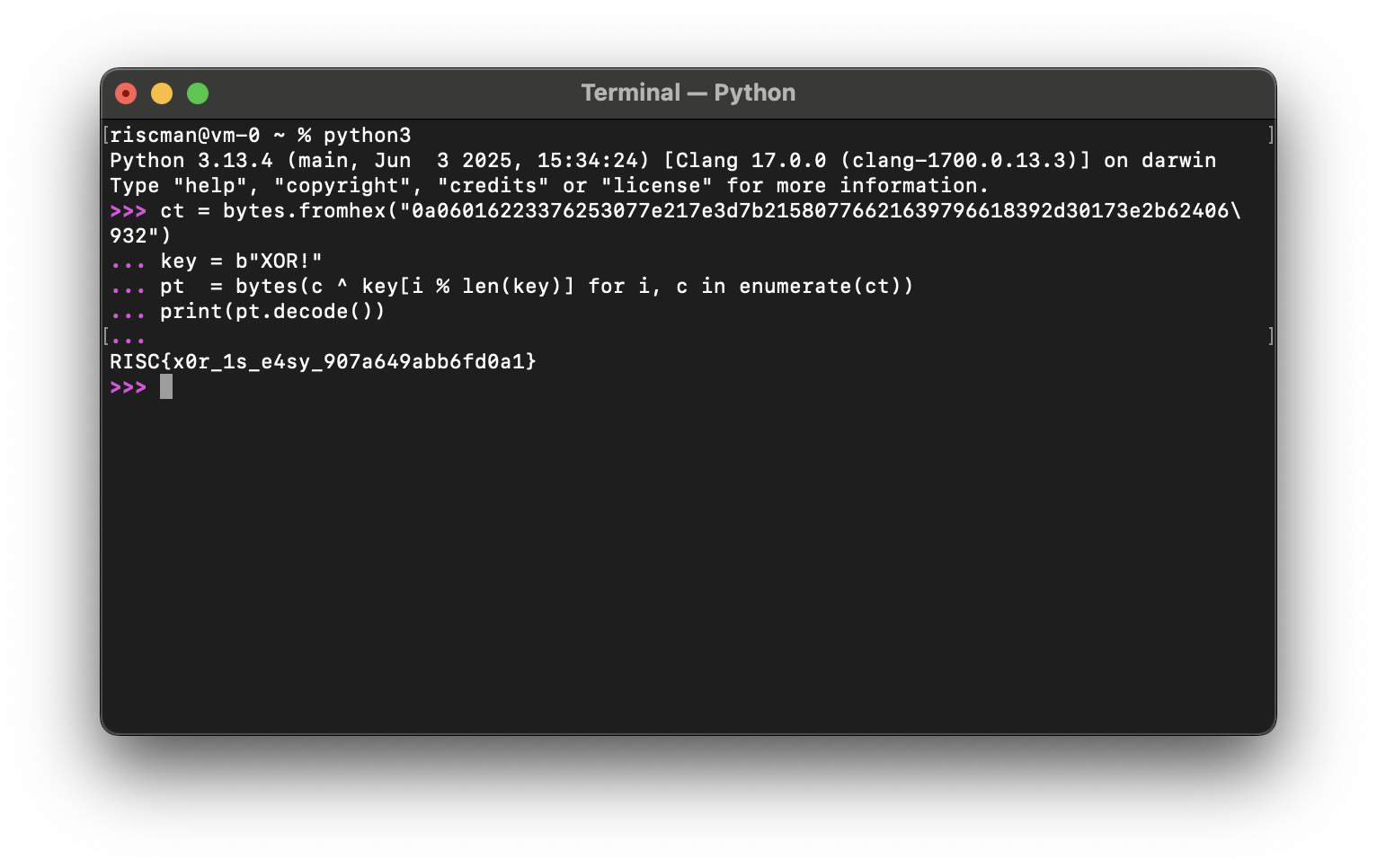
RISC{x0r_1s_e4sy_907a649abb6fd0a1}